Fall 2024 | ETHZ 101-0250-00

Solving partial differential equations in parallel on GPUs

by   Ludovic Räss,   Mauro Werder,   Samuel Omlin &
Ivan Utkin



Lecture 1

Welcome to ETH's course 101-0250-00L on solving partial differential equations (PDEs) in parallel on graphical processing units (GPUs) with the Julia language.

Agenda
💡 Welcome words & The small print
📚 Why GPU computing
💻 Intro to Julia
🚧 Exercises:

  • Numerical solutions

  • Predictive modelling

  • Visualisation

Content

  1. Lecture 1
  2. Solving partial differential equations in parallel on GPUs
    1. The Team
    2. Logistics
    3. Grading
    4. Computing
    5. Summary
  3. Why solve PDEs on GPUs? The tool for the job
    1. Why solve PDEs on GPUs?
  4. Tool for the job: introduction to Julia
    1. Aside 1: Jupyter Notebooks
    2. Aside 2: What is your previous programming experience?
    3. The Julia programming language
    4. Variables, assignments, and types [5min]
    5. Array exercises [15min]
    6. Control flow [10min]
    7. Functions [15min]
    8. Functions: Multiple dispatch demo
    9. Modules and packages [5min]
    10. This concludes the rapid Julia tour
  5. Exercises - lecture 1
    1. Exercise 1 — Car travel
    2. Exercise 2 — Car travel in 2 dimensions
    3. Exercise 3 — Volcanic bomb
    4. Exercise 4 (optional) — Orbital around a centre of mass
    5. Exercise 5 (optional) — Many volcanic bombs

👉 get started with exercises

💡 Note
This week's homework have to be handed in as Jupyter notebook. See here for details.

Solving partial differential equations in parallel on GPUs

The Team

Logistics

All the information should be available on the course's website:
https://pde-on-gpu.vaw.ethz.ch

If something is missing, let us know so we can add it, or even better, submit a pull request to the course's repository

Discussion & help

Grading

All homework assignements can be done either alone or in groups of two. However, note that every student has to hand in a personal version of the homework.

Computing

Bring your laptop to all lectures!

In the first two lectures we will use JupyterHub. Later you will setup a personal Julia installation.

Summary

Suggestion:
Bookmark https://pde-on-gpu.vaw.ethz.ch

⤴ back to Content

Why solve PDEs on GPUs? The tool for the job

Why solve PDEs on GPUs?

A brief intro about GPU computing:

Propaganda

Why we do it

Predict the evolution of natural and engineered systems.

ice2

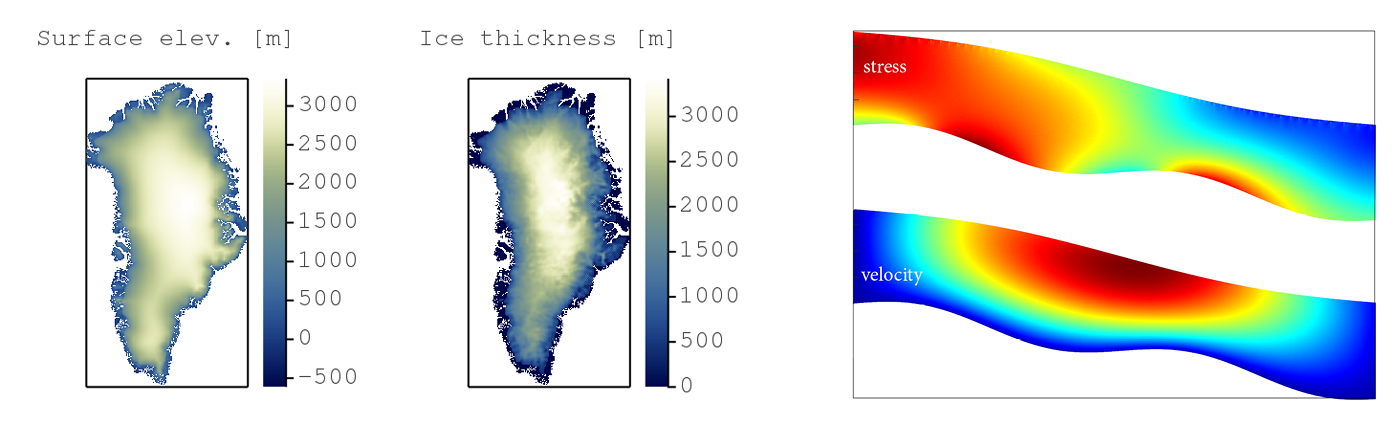
e.g. ice cap evolution, stress distribution, etc...

Physical processes that describe those systems are complex and often nonlinear

👉 a numerical approach is required to solve the mathematical model

A numerical solution means solving a system of (coupled) differential equations

\[ \mathbf{mathematical ~ model ~ → ~ discretisation ~ → ~ solution}\\ \frac{∂C}{∂t} = ... ~ → ~ \frac{\texttt{C}^{i+1} - \texttt{C}^{i}}{\texttt{∆t}} = ... ~ → ~ \texttt{C} = \texttt{C} + \texttt{∆t} \cdot ... \]

Solving PDEs is computationally demanding

\[ \frac{∂C}{∂t} = -\frac{(C-C_{eq})}{ξ} \]

but...

\[ \frac{∂C}{∂t} = D~ \left(\frac{∂^2C}{∂x^2} + \frac{∂^2C}{∂y^2} \right) \]

Computational costs increase

Use parallel computing to address this:

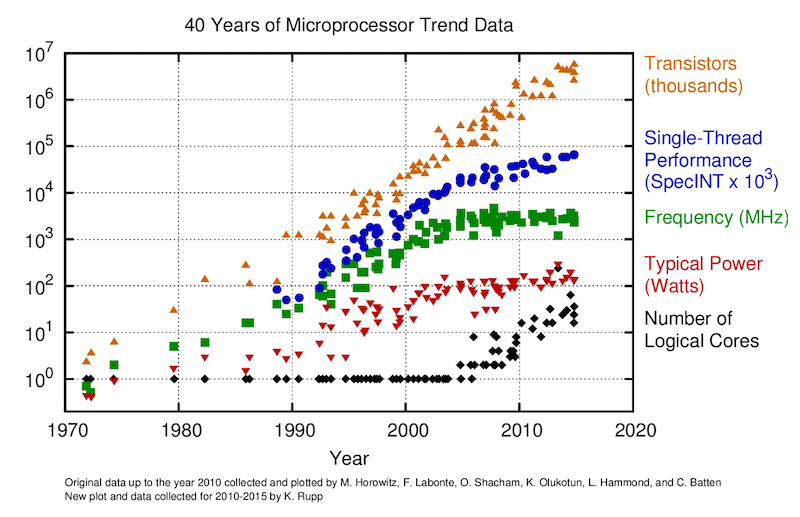
mem_wall

GPUs are massively parallel devices

cpu_gpu_evo

👉 We are memory bound: requires to re-think the numerical implementation and solution strategies

Why it is cool

julia-gpu

GPU are cool

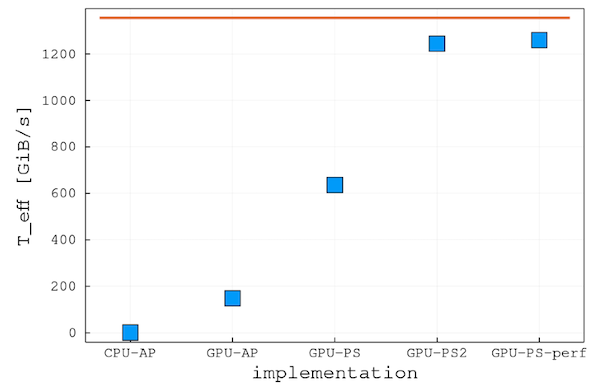
perf_gpu

titan_node

Julia is cool

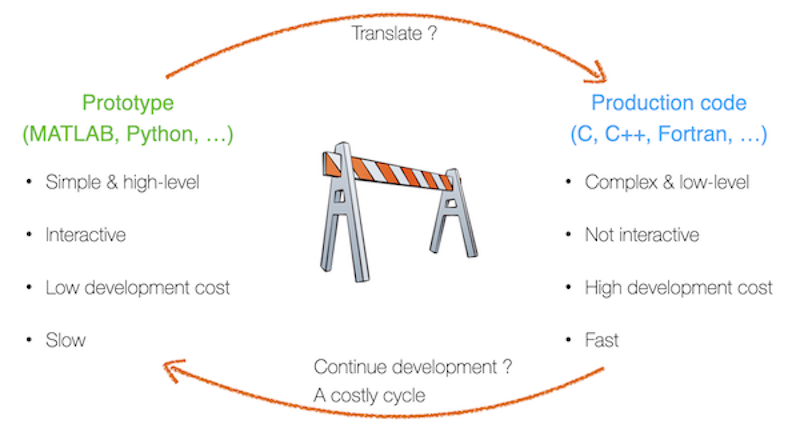
Solution to the "two-language problem"

two_lang

Backend agnostic:

Interactive:

Examples from current research

⤴ back to Content

Tool for the job: introduction to Julia

julia-logo

Aside 1: Jupyter Notebooks

These slides are a Jupyter notebook; a browser-based computational notebook.

💡 Note
You can follow the lecture along live from the Moodle-based JupyterHub server.

Code cells are executed by putting the cursor into the cell and hitting shift + enter. For more info see the documentation.

Aside 2: What is your previous programming experience?

  1. Julia

  2. Matlab, Python, Octave, R, ...

  3. C, Fortran, ...

  4. Pascal, Java, C++, ...

  5. Lisp, Haskell, ...

  6. Assembler

  7. Coq, Brainfuck, ...

Survery for you to fill in now (click or scan, 3min):

survey

The Julia programming language

Julia is a modern, interactive, and high performance programming language. It's a general purpose language with a bend on technical computing.

julia-logo

What does Julia look like

An example solving the Lorenz system of ODEs:

using Plots

function lorenz(x)
    σ = 10
    β = 8/3
    ρ = 28
    [σ*(x[2]-x[1]),
     x[1]*(ρ-x[3]) - x[2],
     x[1]*x[2] - β*x[3]]
end

# integrate dx/dt = lorenz(t,x) numerically for 500 steps
dt = 0.01
x₀ = [2.0, 0.0, 0.0]
out = zeros(3, 500)
out[:,1] = x₀
for i=2:size(out,2)
    out[:,i] = out[:,i-1] + lorenz(out[:,i-1]) * dt
end

Yes, this takes a bit of time... Julia is Just-Ahead-of-Time compiled. I.e. Julia is compiling.

And its solution plotted

plot(out[1,:], out[2,:], out[3,:])

lorenz

Julia in brief

Julia 1.0 released 2018, now at version 1.10

Features:

The two language problem

One language to prototype – one language for production

One language for the users – one language for under-the-hood

Code stats for PyTorch and TensorFlow: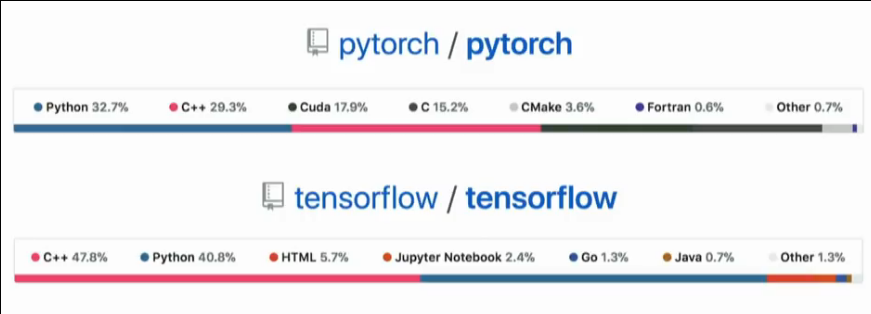

The two language problem

Prototype/interface language:

Production/fast language:

Julia solves the two-language problem

Julia is:

and also:

Code stats for PyTorch, TensorFlow and Flux.jl:

Let's get our hands dirty!

Fire up your JupyterHub, either via the Moodle page, or directly via this link.

[Brief explanation on JupyterHub]

This notebook you can get onto your JupyterHub by

wget https://raw.githubusercontent.com/eth-vaw-glaciology/course-101-0250-00/main/slide-notebooks/notebooks/l1_3-julia-intro.ipynb

Open it by clicking on it in the sidebar.

Let's get our hands dirty!

We will now look at

The documentation of Julia is good and can be found at https://docs.julialang.org; although for learning it might be a bit terse...

There are also tutorials, see https://julialang.org/learning/.

Furthermore, documentation can be gotten with ?xyz

# ?cos

Variables, assignments, and types [5min]

https://docs.julialang.org/en/v1/manual/variables/

a = 4
b = "a string"
c = b # now b and c bind to the same value

Conventions:

Variables: Unicode

From https://docs.julialang.org/en/v1/manual/variables/:

Unicode names (in UTF-8 encoding) are allowed:

julia> δ = 0.00001
1.0e-5

julia> 안녕하세요 = "Hello"
"Hello"

In the Julia REPL and several other Julia editing environments, you can type many Unicode math symbols by typing the backslashed LaTeX symbol name followed by tab. For example, the variable name δ can be entered by typing \delta-tab, or even α̂⁽²⁾ by \alpha-tab-\hat- tab-\^(2)-tab. (If you find a symbol somewhere, e.g. in someone else's code, that you don't know how to type, the REPL help will tell you: just type ? and then paste the symbol.)

#

Basic datatypes

1     # 64 bit integer (or 32 bit if on a 32-bit OS)
1.5   # Float64
1//2  # Rational
typeof(1.5)
"a string", (1, 3.5) # and tuple
[1, 2, 3,] # array of eltype Int
Dict("a"=>1, "b"=>cos)

Array exercises [15min]

We will use arrays extensively in this course.

Datatypes belonging to AbstactArrays:

Task: assign two vectors to a, and b and the concatenate them using ;:

a = [2, 3]
b = [4, 5]
[a ; b]

Add new elements to the end of Vector b (hint look up the documentation for push!)

push!(b, 1)
push!(b, 3, 4)

Array exercises

Concatenate a Range, say 1:10, with a Vector, say [4,5]:

[1:10; [4,5]]

Make a random array of size (3,3). Look up ?rand. Assign it to a

a = rand(3,3)

Array exercise: indexing

Access element [1,2] and [2,1] of Matrix a (hint use []):

a[1,2], a[2,1]

Put those two values into a vector

[ a[1,2], a[2,1] ]

Linear vs Cartesian indexing, access the first element:

a[1]
a[1,1]

Access the last element (look up ?end) both with linear and Cartesian indices

a[end]
a[end, end]

Array exercise: indexing by ranges

Access the last row of a (hint use 1:end)

a[end, 1:end]

Access a 2x2 sub-matrix

a[1:2, 1:2]

Array exercises: variable bindings and views

What do you make of

a = [1 4; 3 4] # note, this is another way to define a Matrix
c = a
a[1, 2] = 99
@assert c[1,2] == a[1,2]

Type your answer here (to start editing, double click into this cell. When done shift+enter):

Both variables `a` and `c` refer to the same "thing".  Thus updating the array via one will show in the other.

Array exercises: variable bindings and views

An assignment binds the same array to both variables

c = a
c[1] = 8
@assert a[1]==8 # as c and a are the same thing
@assert a===c  # note the triple `=`

Views vs copies:

In Julia indexing with ranges will create a new array with copies of the original's entries. Consider

a = rand(3,4)
b = a[1:3, 1:2]
b[1] = 99
@assert a[1] != b[1]

Array exercises: variable bindings and views

But the memory footprint will be large if we work with large arrays and take sub-arrays of them.

Views to the rescue

a = rand(3,4)
b = @view a[1:3, 1:2]
b[1] = 99

check whether the change in b is reflected in a:

@assert a[1] == 99

A small detour: types

All values have types as we saw above. Arrays store in their type what type the elements can be.

Arrays which have concrete element-types are more performant!

typeof([1, 2]), typeof([1.0, 2.0])

Aside, they also store their dimension in the second parameter.

The type can be specified at creation

String["one", "two"]

Create an array taking Int with no elements. Push 1, 1.0 and 1.5 to it. What happens?

a = Int[]
push!(a, 1) ## works
push!(a, 1.0) ## works
push!(a, 1.5) ## errors as 1.5 cannot be converted to an Int

Make an array of type Any (which can store any value). Push a value of type Int and one of type String to it.

a = []
push!(a, 5)
push!(a, "a")

Try to assgin 1.5 to the first element of an array of type Array{Int,1}

[1][1] = 1.5 ## errors

Array exercises

Create a uninitialised Matrix of size (3,3) and assign it to a. First look up the docs of Array with ?Array

a = Array{Any}(undef, 3, 3)

Test that its size is correct, see size

size(a)

Array exercises: ALL DONE

The rest about Arrays you will learn-by-doing.

Control flow [10min]

Julia provides a variety of control flow constructs, of which we look at:

Conditional evaluation

Read the first paragraph of https://docs.julialang.org/en/v1/manual/control-flow/#man-conditional-evaluation (up to "... and no further condition expressions or blocks are evaluated.")

Write a test which looks at the start of the string in variable a (?startswith) and sets b accordingly. If the start is

a = "Where are the flowers"
if startswith(a, "Wh")
  b = "Likely a question"
elseif startswith(a, "The")
  b = "Likely a noun"
else
  b = "no idea"
end

Conditional evaluation: the "ternary operator" ?

Look up the docs for ? (i.e. evaluate ??)

Re-write using ?

if a > 5
    "really big"
else
    "not so big"
end
a > 5 ? "really big" : "not so big"

Short circuit operators && and ||

Read https://docs.julialang.org/en/v1/manual/control-flow/#Short-Circuit-Evaluation

Explain what this does

a < 0 && error("Not valid input for `a`")

Type your answer here (to start editing, double click into this cell. When done shift+enter):

If a < 0 evaluates to true then the bit after the && is evaluated too, i.e. an error is thrown. Otherwise, only a < 0 is evaluated and no error is thrown.

Loops: for and while

https://docs.julialang.org/en/v1/manual/control-flow/#man-loops

for i = 1:3
    println(i)
end

for i in ["dog", "cat"] ## `in` and `=` are equivalent for writing loops
    println(i)
end

i = 1
while i<4
    println(i)
    i += 1
end

Functions [15min]

Functions can be defined in Julia in a number of ways. In particular there is one variant more suited to longer definitions, and one for one-liners:

function f(a, b)
   return a * b
end
f(a, b) = a * b

Defining many, short functions is typical in good Julia code.

Read https://docs.julialang.org/en/v1/manual/functions/ up to an including "The return Keyword"

Functions: exercises

Define a function in long-form which takes two arguments. Use some if-else statements and the return keyword.

function fn(a, b)
  if a> b
    return a
  else
    return b
  end
end

Functions: exercises

Re-define the map function. First look up what it does ?map, then create a mymap which does the same. Map sin over the vector 1:10.

(Note, this is a higher-order function: a function which take a function as a argument)

mymap(fn, a) = [fn(aa) for aa in a]
mymap(sin, 1:10)

Functions: dot-syntax

This is really similar to the map function, a short-hand to map/broadcast a function over values.

Exercise: apply the sin function to a vector 1:10:

sin.(1:10)

Broadcasting will extend row and column vectors into a matrix. Try (1:10) .+ (1:10)' (Note the ', this is the transpose operator)

(1:10) .+ (1:10)'

Functions: dot-syntax exercise

Evaluate the function sin(x) + cos(y) for x = 0:0.1:pi and y = -pi:0.1:pi. Remember to use '.

x,y = 0:0.1:pi, -pi:0.1:pi
sin.(x) .+ cos.(y')

Functions: anonymous functions

So far our function got a name with the definition. They can also be defined without name.

Read https://docs.julialang.org/en/v1/manual/functions/#man-anonymous-functions

Map the function f(x,y) = sin(x) + cos(x) over 1:10 but define it as an anonymous function.

map(x -> sin(x) + cos(x), 1:10)

Key feature: multiple dispatch functions

OO:

Multiple dispatch:

very natural for mathematical programming

JuliaCon 2019 presentation on the subject by Stefan Karpinski (co-creator of Julia):

"The Unreasonable Effectiveness of Multiple Dispatch"

Functions: Multiple dispatch demo

struct Rock end
struct Paper end
struct Scissors end
### of course structs could have fields as well
# struct Rock
#     color
#     name::String
#     density::Float64
# end

# define multi-method
play(::Rock, ::Paper) = "Paper wins"
play(::Rock, ::Scissors) = "Rock wins"
play(::Scissors, ::Paper) = "Scissors wins"
play(a, b) = play(b, a) # commutative

play(Scissors(), Rock())

Multiple dispatch demo

Can easily be extended later

with new type:

struct Pond end
play(::Rock, ::Pond) = "Pond wins"
play(::Paper, ::Pond) = "Paper wins"
play(::Scissors, ::Pond) = "Pond wins"

play(Scissors(), Pond())

with new function:

combine(::Rock, ::Paper) = "Paperweight"
combine(::Paper, ::Scissors) = "Two pieces of papers"
# ...

combine(Rock(), Paper())

Multiple dispatch makes Julia packages very composable!

This is a key characteristic of the Julia package ecosystem.

Modules and packages [5min]

Modules can be used to structure code into larger entities, and be used to divide it into different name spaces. We will not make much use of those, but if interested see https://docs.julialang.org/en/v1/manual/modules/

Packages are the way people distribute code and we'll make use of them extensively. In the first example, the Lorenz ODE, you saw

using Plots

This statement loads the package Plots and makes its functions and types available in the current session and use it like so:

using Plots
plot( (1:10).^2 )

Packages

Note package installation does not work on the moodle-Jupyterhub. But it will work on your local installation.

All public Julia packages are listed on https://juliahub.com/ui/Packages.

You can install a package, say Example.jl (a tiny example package) by

using Pkg
Pkg.add("Example")
using Example
hello("PDE on GPU class")

In the REPL, there is also a package-mode (hit ]) which is for interactive use.

# Install a package (not a too big one, Example.jl is good that way),
# use it, query help on the package itself:

This concludes the rapid Julia tour

There are many more features of Julia for sure but this should get you started, and setup for the exercises. (Let us know if you feel we left something out which would have been helpful for the exercises).

Remember you can self-help with:

⤴ back to Content

Exercises - lecture 1

Exercise 1 — Car travel

👉 Download the notebook to get started with this exercise!

⚠️ Warning!
Write a monolithic Julia script to solve this exercise in a Jupyter notebook and hand it in on Moodle (more).

The goal of this exercise is to familiarise with:

A car cruises on a straight road at given speed \(\mathrm{V = 113}\) km/h for 16 hours, making a U-turn after a distance \(\mathrm{L = 200}\) km. The car speed is defined as the change of position its \(x\) per time \(t\):

\[ V = \frac{\partial x}{\partial t} \]

In the above derivative, \(\partial x\) and \(\partial t\) are considered infinitesimal - a representation it is not possible to handle within a computer (as it would require infinite amount of resources). However, we can discretise this differential equation in order to solve it numerically by transforming the infinitesimal quantities into discrete increments:

\[ V = \frac{\partial x}{\partial t} \approx \frac{\Delta x}{\Delta t} = \frac{x_{t+\Delta t}-x_t}{\Delta t}~, \]

where \(\Delta x\) and \(\Delta t\) are discrete quantities. This equation can be re-organised to return an explicit solution of the position \(x\) at time \(t+\Delta t\):

\[ x_{t+\Delta t} = x_{t} + V \Delta t~. \]

  1. Based on this equation, your task is to setup a numerical model to predict the position of the car as function of time. In order not to start from scratch this time, you can complete the code draft below, filling in the relevant quantities in following order:

using Plots

@views function car_travel_1D()
    # Physical parameters

    # Numerical parameters

    # Array initialisation

    # Time loop

    # Visualisation

    return
end

car_travel_1D()

  1. Implement a condition to allow you doing U-turns whenever you reach the position \(x=0\) or \(x=200\).

The sample code you can use to get started looks like:

using Plots

@views function car_travel_1D()
    # Physical parameters
    V     =         # speed, km/h
    L     =         # length of segment, km
    ttot  =         # total time, h
    # Numerical parameters
    dt    = 0.1            # time step, h
    nt    = Int(cld(ttot, dt))  # number of time steps
    # Array initialisation
    T     =
    X     =
    # Time loop
    for it = 2:nt
        T[it] = T[it-1] + dt
        X[it] =   # move the car
        if X[it] > L
                # if beyond L, go back (left)
        elseif X[it] < 0
                # if beyond 0, go back (right)
        end
    end
    # Visualisation
    display(scatter(T, X, markersize=5,
                    xlabel="time, hrs", ylabel="distance, km",
                    framestyle=:box, legend=:none))
    return
end

car_travel_1D()

Note that you can extend the first code (from step 1) to include the U-turns and use your final code to reply to the question.

Question 1

Once the code is running, test various time step increments 0.1 < dt < 1.0 and briefly comment on your findings.

⤴ back to Content

Exercise 2 — Car travel in 2 dimensions

👉 Download the notebook to get started with this exercise!

⚠️ Warning!
Write a monolithic Julia script to solve this exercise in a Jupyter notebook and hand it in on Moodle (more).

The goal of this exercise is to familiarise with:

Based on the experience you acquired solving the Exercise 1 we can now consider a car moving within a 2-dimensional space. The car still travels at speed \(V=113\) km/h, but now in North-East or North-West direction. The West-East and South-North directions being the \(x\) and \(y\) axis, respectively. The car's displacement in the West-East directions is limited to \(L=200\) km. The speed in the North direction remains constant.

Starting from the 1D code done in Exercise 1, work towards adding the second spatial dimension. Now, the car's position \((x,y)\) as function of time \(t\) has two components.

💡 Note

  • Split velocity magnitude \(V\) into \(x\) and \(y\) component

  • Use sind() or cosd() functions if passing the angle in deg instead of rad

  • Use two vectors or an array to store the car's coordinates

  • Define the y-axis extend in the plot ylims=(0, ttot*Vy)

Question 1

Visualise graphically the trajectory of the travelling car for a simulation with time step parameter defined as dt = 0.1.

⤴ back to Content

Exercise 3 — Volcanic bomb

👉 Download the notebook to get started with this exercise!

⚠️ Warning!
Write a monolithic Julia script to solve this exercise in a Jupyter notebook and hand it in on Moodle (more).

The goal of this exercise is to consolidate:

You will now simulate the trajectory of a volcanic bomb that got ejected during a volcanic eruption. The ejection speed is given by the horizontal and vertical velocity components

\[ V_x = \frac{\partial x}{\partial t}\\[10pt] V_y = \frac{\partial y}{\partial t} \]

Once ejected, the volcanic bomb is subject to gravity acceleration \(g\). Air friction will be neglected. Acceleration being defined as the change of velocity over time, we obtain the following update rule:

\[ \frac{\partial V_y}{\partial t}=-g \]

These equations define a mathematical model describing the kinematics of the volcanic bomb. You may remember from your studies how to solve those equation analytically; however we'll here focus on a numerical solution using a similar approach as for the previous exercises. The \(x\) and \(y\) location of the bomb as function of time can be obtained based on updating previous values using the definition of velocity:

\[ x_{t+\Delta t} = x_{t} + V_x \Delta t~,\\[5pt] y_{t+\Delta t} = y_{t} + V_y(t) \Delta t~. \]

And because of gravity acceleration, the \(V_y\) velocity evolution can be obtained according to

\[ V_{y,t+\Delta t} = V_{y,t} - g \Delta t~. \]

The 3 equations above represent the discretised form of the 3 first equations and should be used to solve the problem numerically. The initial position of the volcanic bomb \((x_0, y_0)=(0,480)\) m. The magnitude of the ejection speed is of 120 m/s and the angle \(\alpha = 60°\). The simulation stops when the volcanic bomb touches the ground (\(y=0\)).

💡 Note

  • Modify the code from exercise 2 to, in addition, account for the change of Vy with time

  • Use e.g. a break statement to exit the loop once the bomb hits the ground

Question 1

Report the height of the volcanic bomb at position \(x=900\) m away from origin.

⤴ back to Content

Exercise 4 (optional) — Orbital around a centre of mass

👉 Download the notebook to get started with this exercise!

⚠️ Warning!
Write a monolithic Julia script to solve this exercise in a Jupyter notebook and hand it in on Moodle (more).

The goal of this exercise is to consolidate:

The goal of this exercise is to reproduce an orbital around a fixed centre of mass, which is also the origin of the coordinate system (e.g. Earth - Sun). To solve this problem, you will have to know about the definition of velocity, Newton's second law and universal gravitation's law:

\[ \frac{dr_i}{dt}=v_i \\[10pt] \frac{dv_i}{dt}=\frac{F_i}{m} \\[10pt] F_i = -G\frac{mM}{|r_i|^2}\frac{r_i}{|r_i|}~, \]

where \(r_i\) is the position vector, \(v_i\) the velocity vector, \(F_i\) the force vector, \(G\) is the gravitational constant, \(m\) is the mass of the orbiting object, \(M\) is the mass of the centre of mass and \(|r_i|\) is the norm of the position vector.

The sample code you can use to get started looks like:

using Plots

@views function orbital()
    # Physics
    G    = 1.0
    # TODO - add physics input
    tt   = 6.0
    # Numerics
    dt   = 0.05
    # Initial conditions
    xpos = ??
    ypos = ??
    # TODO - add further initial conditions
    # Time loop
    for it = 1:nt
        # TODO - Add physics equations
        # Visualisation
        display(scatter!([xpos], [ypos], title="$it",
                         aspect_ratio=1, markersize=5, markercolor=:blue, framestyle=:box,
                         legend=:none, xlims=(-1.1, 1.1), ylims=(-1.1, 1.1)))
    end
    return
end

orbital()

Question 1

For a safe start, set all physical parameters \((G, m, M)\) equal to 1, and use as initial conditions \(x_0=0\) and \(y_0=1\), and \(v_x=1\) and \(v_y=0\). You should obtain a circular orbital.

Report the last \((x,y)\) position of the Earth for a total time of tt=6.0 with a time step dt=0.05.

💡 Note

  • \(r_i=[x,y]\)

  • \(|r_i|=\sqrt{x^2 + y^2}\)

  • \(r_i/|r_i|\) stands for the unity vector (of length 1) pointing from \(m\) towards \(M\)

Question 2

Head to e.g. Wikipedia and look up for approximate of real values and asses whether the Earth indeed needs ~365 days to achieve one rotation around the Sun.

⤴ back to Content

Exercise 5 (optional) — Many volcanic bombs

👉 Download the notebook to get started with this exercise!

⚠️ Warning!
Write a monolithic Julia script to solve this exercise in a Jupyter notebook and hand it in on Moodle (more).

The goal of this exercise is to consolidate:

The goal is to extend the volcanic bomb calculator (exercise 3) to handle nb bombs.

To do so, start from the script you wrote to predict the trajectory of a single volcanic bomb and extend it to handle nb bombs.

Declare a new variable for the number of volcanic bombs

nb = 5 # number of volcanic bombs

Then, replace the vertical angle of ejection α to randomly vary between 60° and 120° with respect to the horizon for each bomb. Keep the magnitude of the ejection velocity as before, i.e. \(V=120\) m/s.

💡 Note
Use the randn() function to generate random numbers normally distributed.

All bombs have the same initial location \((x=0, y=480)\) as before.

Implement the necessary modifications in the time loop in order to update the position of all volcanic bombs correctly.

Ensure the bombs stop their motion once they hit the ground (at position \(y=0\)).

Question 1

Report the total time it takes for the last, out of 5, volcanic bombs to hit the ground and provide a figure that visualise the bombs' overall trajectories.

Question 2

Repeat the same exercise as in Question 1, but vectorise all your code, i.e. make use of broadcasting capabilities in Julia (using . operator) to only have a single loop for advancing in time.

⤴ back to Content

Edit this page on
Last modified: November 18, 2024. Website built with Franklin.jl and the Julia programming language.